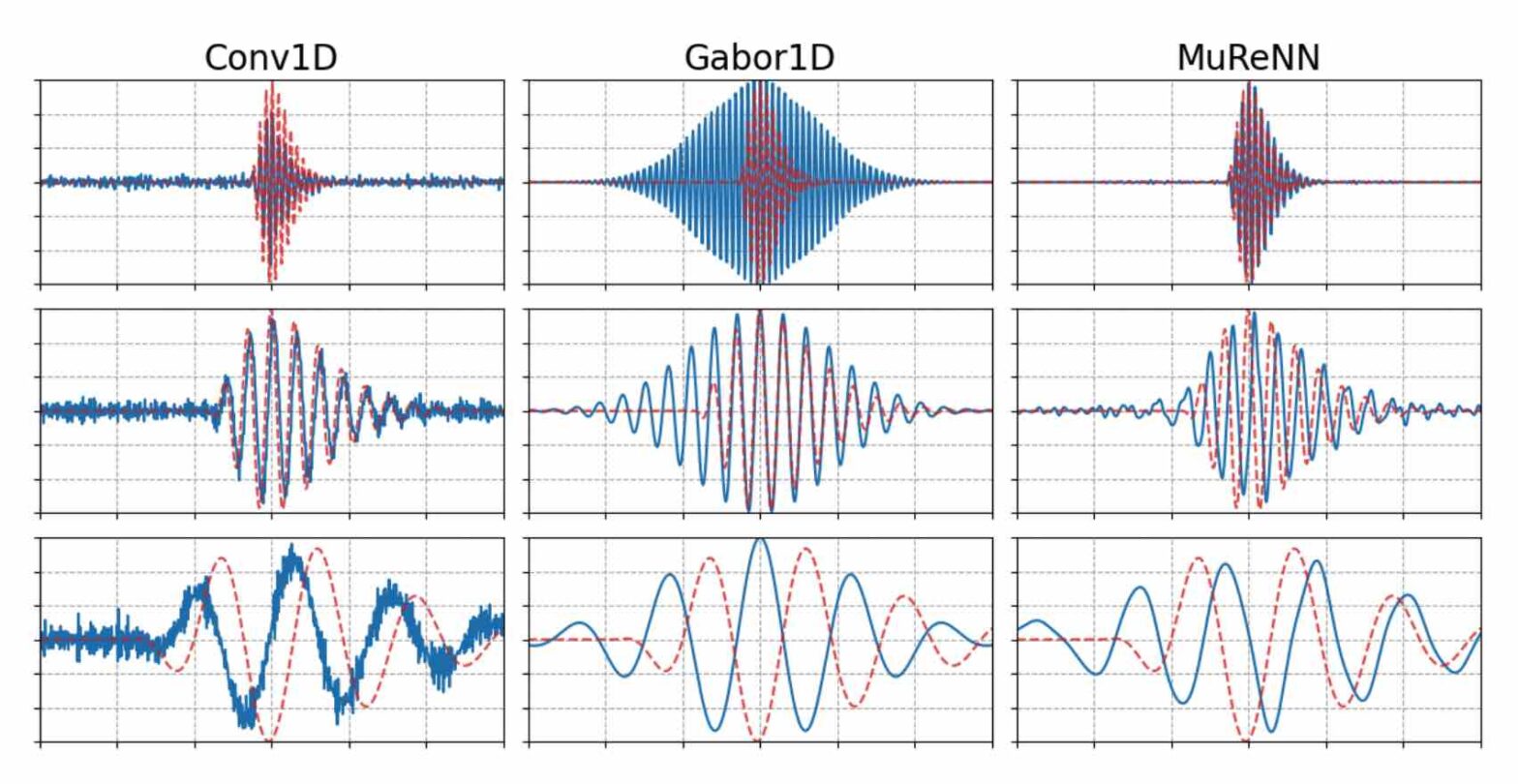
Fitting Auditory Filterbanks with Multiresolution Neural Networks
Communications dans un congrès
Auteurs : Vincent Lostanlen, Daniel Haider, Han Han, Mathieu Lagrange, Peter Balazs, Martin Ehler.
Conférence : IEEE Workshop on Applications of Signal Processing to Acoustics and Audio (WASPAA 2023)
Date de publication : 2023
Convolutional neural networkDigital filtersFilterbanksMultiresolution analysisPsychoacoustics